Answer:
Step-by-step explanation:
Refractive index f the medium, n = t
Let the angle of incidence is i
(a) As given in the question, the angle of refraction is half of angle of incidence.
Let the angle of refraction is r
r = i / 2
By use of Snell's law

By substituting the values, we get
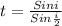
By using the formula of trigonometry
Sin2Ф = 2 SinФ CosФ
So,

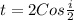
(b) For glass, the value of refractive index is 1.5, so the above expression becomes
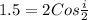
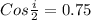
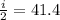
i = 82.8°