Question

a class of 30 students, 2 students did not borrow any books from the library, 12 students each borrowed 1 book, 10 students each borrowed 2 books, and the rest of the students each borrowed at least 3 books. If the average (arithmetic mean) number of books borrowed per student was 2, what is the maximum number of books that any single student could have borrowed?

Answer 1

13

Explanation:

It's given that 2 students borrowed 0 books, 12 borrowed 1 book, 10 borrowed 2 books, and 6 borrowed 3 or more books. The average of books per student is 2.

To analyse the problem, let a, b, c, d, e, and f be the number of books borrowed by each of the 6 students who borrowed 3 or more, as the maximum must be one of those 6.

The average is calculated by adding up the borrowed books from all students, and then diving it 30 (the number of students). This would be :

`(2*0+12*1+10*2+(a+b+c+d+e+f))/(30) =2`

`(32+(a+b+c+d+e+f))/(30) =2`

`\ 32+a+b+c+d+e+f=60`

`\ a+b+c+d+e+f=28`

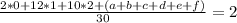
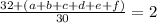
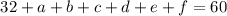
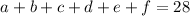
The maximum value for any student would be found when all other 5 students borrowed the minimum, which is 3 in this case. So set them all but one equal to 3 :

`\ 3+3+3+3+3+f=28`

`\ 15+f=28`

`\ f=28 - 15=13`

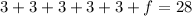
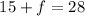
So the maximum is 13.