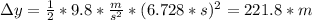Answer:
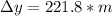
Explanation:
The distance that the rock has traveled to reach the ground (also, the height of the cliff) can be calculated using:
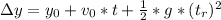
 is our incognit
is our incognit
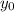 is the starting position of the rock, we'll define it as 0
is the starting position of the rock, we'll define it as 0
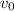 is the starting velocity of the rock, it is 0 since it starts from rest
is the starting velocity of the rock, it is 0 since it starts from rest
g is the acceleration of gravity
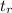 is the time it took the rock reaching the ground
is the time it took the rock reaching the ground
Also, we can model the "movement" of sound as it follows:

where:
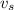 is the velocity of sound :330m/s
is the velocity of sound :330m/s
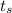 is the time it took the sound travelling to the top of the cliff
is the time it took the sound travelling to the top of the cliff
using the first and the second equation, and the fact that
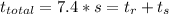 we get to:
we get to:
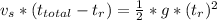
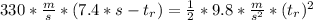
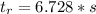 (we get to values for tr since the equation is quadratic, the correct one is the positive)
(we get to values for tr since the equation is quadratic, the correct one is the positive)
Now that we have
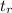 we can use it to calculate
we can use it to calculate
 and determine the height of the cliff:
and determine the height of the cliff: