Answer: 0.3042
Step-by-step explanation:
Let A and B are the events to that job done by Printer I and Printer II respectively.
Given : P(A)=0.40 P(B)=0.60
Printing time of Printer I is Exponential with the mean of 2 minutes.
i.e. average number of job done in one minute:
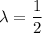
The cumulative distribution function (CDF) for exponential distribution:-
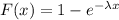 , where
, where
 is the mean.
is the mean.
Then, the cumulative distribution function (CDF) for Printer I:-
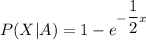
i.e.
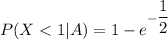
Printing time of Printer II is Uniform between 0 minutes and 5 minutes.
The cumulative distribution function (CDF) for uniform distribution in interval (a,b) :-

Then,
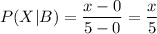
i.e.
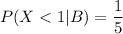
Now, the required probability :-
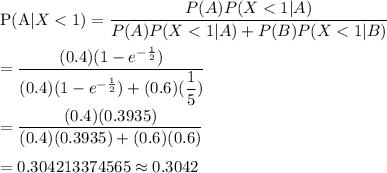
Hence, the required probability = 0.3042