Question

Which of the following describes the behavior of the function f at point P?

a.The value of f changes from positive to negative.
b.The rate of change of f changes from decreasing to increasing.
c.The rate of change of f is 0. f changes from increasing at an increasing rate to increasing at a decreasing rate.
d.f changes from increasing at a decreasing rate to increasing at an increasing rate.

Answer 1

The correct answer is option 'b': The rate of change of f changes from decreasing to increasing.

Step-by-step explanation:

In differential calculus the behavior of any smooth function can be understood on the basis of slope of function alone. As slope of the function is the representation of rate of change of function.

Mathematically

Given
`f(x)` as any function we have

1) if
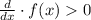`(d)/(dx)\cdot f(x)>0` then the function is increasing

2) 1) if
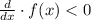`(d)/(dx)\cdot f(x)<0` then the function is decreasing

3) 1) if
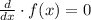`(d)/(dx)\cdot f(x)=0` then the function reaches a critical point.

Thus the nature of the function at any point is specified by the nature of the differential at the point provided the function is defined at that point at which we need to check the behavior.