Question

What is the sum of the first 70 consecutive odd numbers? Explain.

Answer 1

The sum of the first n odd numbers is n squared! So, the short answer is that the sum of the first 70 odd numbers is 70 squared, i.e. 4900.

Allow me to prove the result: odd numbers come in the form 2n-1, because 2n is always even, and the number immediately before an even number is always odd.

So, if we sum the first N odd numbers, we have

`\displaystyle \sum_(i=1)^N 2i-1 = 2\sum_(i=1)^N i - \sum_(i=1)^N 1`

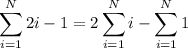
The first sum is the sum of all integers from 1 to N, which is N(N+1)/2. We want twice this sum, so we have

`\displaystyle 2\sum_(i=1)^N i = 2\cdot(N(N+1))/(2)=N(N+1)`

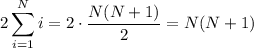
The second sum is simply the sum of N ones:

`\underbrace{1+1+1\ldots+1}_{N\text{ times}}=N`

So, the final result is

`\displaystyle \sum_(i=1)^N 2i-1 = 2\sum_(i=1)^N i - \sum_(i=1)^N 1 = N(N+1)-N = N^2+N-N = N^2`

which ends the proof.