Question

If ∫−1−4f(x)dx=0 and ∫31g(x)dx=3, what is the value of ∫∫Df(x)g(y)dA where D is the square: −4≤x≤−1, 1≤y≤3?

Answer 1

0

Explanation:

From your problem, we have to extract the information that are important from the first two intregrals so we can solve the double integral.

`\int\limits^(-1)_(-4) {f(x)} \, dx = 0`

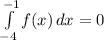
We also have that:

`\int\limits^(3)_(1) {g(x)} \, dx = 3`

---------------------------------

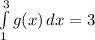
With this, now we can solve the double integral.

Since the limits of integration are constant, i can use dA both as dydx or dxdy. I am going to use dydx.

So the double integral will be:

`\int \limits^(-1)_(-4) \int \limits^(3)_(1) {g(y)} {f(x)} dy dx\`

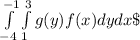
We solve a double integral from the inside to the outside, so the first integral we solve is:

`\int \limits^(3)_(1) \y g(y) \x f(x) dy`

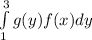
f is a function of x and we are integrating dy, so this means that f is a constant. Our integral now is this:

`\x f(x) \int \limits^(3)_(1) \y g(y) dy`

From above, we have that

`\int \limits^(3)_(1) \x g(x) dx = 3`

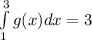
So,

`\int \limits^(3)_(1) \y g(y) dy = 3`

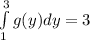
Now we have to solve the outside integral:

`3\int\limits^(-1)_(-4) {f(x)} \, dx`

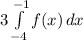
We know that

`\int\limits^(-1)_(-4) {f(x)} \, dx = 0`

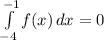
So the double integral will be 0