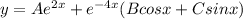Question

Find the general solution of y''' + 6y'' + y' − 34y = 0 if it is known that y1 = e−4x cos(x) is one solution.

Answer 1

Explanation:

Given is a differential equation of III order,

`y''' + 6y'' + y' - 34y = 0`

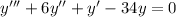
The characteristic equation would be cubic as

`m^3+6m^2+m-34=0`

By trial and error, we find that

`f(2) = 2^3+6(2^2)+2-34 =0\\`

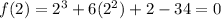
Thus m=2 is one solution

Since given that
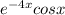`e^(-4x) cos x`is one solution we get

m = -4+i and hence other root is conjugate
`m=-4-i`

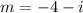
Hence general solution would be

`y=Ae^(2x) +e^(-4x) (Bcosx +C sinx)`