Question

The gage pressure in a liquid at a depth of 3 m is read to be 50 kPa. Determine the gage pressure in the same liquid at a depth of 9 m.

Answer 1

The gage pressure at a depth of 9 m in the same liquid is approximately 813 kPa.

Step-by-step explanation:

Gauge pressure in a liquid is determined by the depth of the liquid column above the point of measurement. The equation for gauge pressure at a certain depth is given by:

P2 = P1 + ρgh

Where P2 is the gauge pressure at the second depth, P1 is the gauge pressure at the first depth (50 kPa), ρ is the density of the liquid, g is the acceleration due to gravity, and h is the difference in depth between the two points.

Since the density of the liquid is constant throughout, the equation simplifies to:

P2 = P1 + ρgh

Plugging in the values, we have:

P2 = 50 kPa + (900 kg/m³)(9.8 m/s²)(9 m)

Solving for P2, we get a gage pressure of approximately 813 kPa at a depth of 9 m in the same liquid.

Answer 2

The Gauge pressure at 9 meters depth is
`150 \, kPa`

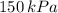
Step-by-step explanation:

Gauge pressure is the difference between absolute pressure and some reference pressure, most commonly atmospheric pressure. The increment in pressure caused by a static fluid is given by:

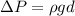`\Delta P = \rho g d` where
`\rho` is the density of the liquid, g is the accleration due to gravity and d is the depth.

Now, we see that
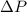`\Delta P` is linearly proportional to d, and we can assume that
`\rho` remains constant, because liquids are usually not compressible.

Given that the greater depth is simply 3 times the smaller depth:

`d_2=3\cdot d_1\\9\,m= 3 \cdot 3\,m`

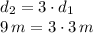
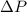`\Delta P` at
`9\, m` of depth will also be three times the gauge pressure at
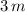`3 \,m` of depth.

We could also have calculated
`\rho` ny using:

`\Delta P = \rho \,g \,d\\\\\rho = (\Delta P)/(g \, d)\\\\\rho = (\Delta P)/(g \, d)= (30 \,kPa)/(9.8 (m)/(s^2)  \, 3\,m)=1020.41 (kg)/(m^3)`

and used this result to calculate the gauge pressure. These are both similar methods that yield the same result