Question

Suppose that f : [a, b] → [a, b] is continuous. Prove that f has a fixed point. That is, prove that there exists c ∈ [a, b] such that f (c) = c.

Answer 1

Explanation:

define the function:

`g(x) = f(x) -x`

As both
`f(x)` and x are continuous functions,
`g(x)` will also be continuous.

Now, what can we say about
`g(a) = f(a) -a`?

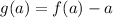we know that
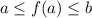`a\leq f(a) \leq b`, thus:

`a-a\leq f(a)-a \leq b-a\\0 \leq g(a) \leq b-a`

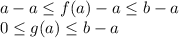
thus
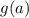`g(a)` is non-negative.

What about
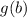`g(b)` ? Again we have:

`a\leq f(b) \leq b\\a-b \leq f(b) -b \leq  0\\a-b \leq g(b) \leq  0`

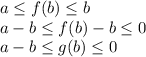
That means that
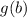`g(b)` is not positive.

Now, we can imagine two cases, either one of
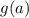`g(a)` or
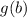`g(b)` is equal to zero, or none of them is. If either of them is equal to zero, we have found a fixed point! In fact, any point
`c` for which
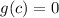`g(c)=0` is a fixed point, because:

`g(c) = 0 \implies f(c) -c = 0 \implies f(c) = c`

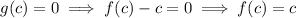
Now, if
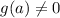`g(a) \\eq  0` and
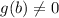`g(b) \\eq 0`, then we have that

`g(a) >0` and
`g(b) < 0`. And by Bolzano's theorem we can assert that there must exist a point c between a and b for which
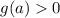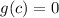`g(c)=0`. And as we have shown before that point would be a fixed point. This completes the proof.