Answer:
The range and domain of this function is [-2, 2]
Explanation:
For the domain it must be fulfilled that
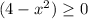 . Then,
. Then,
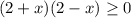 . This expression is true for the values of
. This expression is true for the values of
 that make the factors simultaneously non-negative or non-positive.
that make the factors simultaneously non-negative or non-positive.
Case non-negative factors
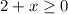 implies that
implies that
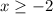 , that is
, that is
![[-2, +\infty]](https://img.qammunity.org/2020/formulas/mathematics/college/j4aj00aqb13zcup17onqkdgvtfdm2nf75b.png)
 implies that
implies that
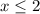 , that is,
, that is,
![(-\infty, 2]](https://img.qammunity.org/2020/formulas/mathematics/college/ge03vfy5tq6zt1hg2uoso3mim3o6iyc200.png) . The intersection of the previous sets is [-2, 2].
. The intersection of the previous sets is [-2, 2].
Case non positive factors
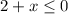 implies that
implies that
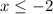 , that is
, that is
![(-\infty, -2]](https://img.qammunity.org/2020/formulas/mathematics/college/b9yo3r4sju7moygcgboe886di27q88eqmr.png)
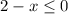 implies that
implies that
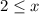 , that is,
, that is,
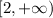 . The intersection of the previous sets is empty.
. The intersection of the previous sets is empty.
Then the domain of the function is [-2, 2]
The range of this function is the domain of its inverse. The inverse of the function is itself, so the range is [-2, 2]