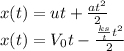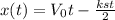Question

The velocity of a particle traveling along a straight line is v = Vo − ks where k is constant. If s=0 when t=0, determine the position and acceleration of the particle as a function of time.

Answer 1

acceleration of the particle as a function of time is given as

`a(t)=-(ks)/(t)`

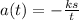
and position of the particle as a function of time is given as

`x(t)=ut+(at^2)/(2) \\x(t)=V_(0)t-((ks(t))/(t)t^2)/(2)`

`x(t)=V_(0)t-(kst)/(2)`

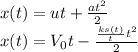
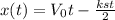
Step-by-step explanation:

we have given,

`v=v_(o)− ks`

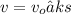
at t=0, s=0

therefore initial velocity,u

u=v=
`V_(o)`

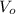
v=u+at.........(1)

we know from first equation of motion

let acceleration at time t be a(t), and position be x(t)

put value of v,u and a in equation 1

we got,

`V_(o)-ks=V_(o)+a(t)t`

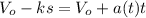
Therefore,acceleration of the particle as a function of time is given as

`a(t)=-(ks)/(t)`

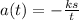
and position of the particle as a function of time is given as

`x(t)=ut+(at^2)/(2) \\x(t)=V_(0)t-((ks)/(t)t^2)/(2)`

`x(t)=V_(0)t-(kst)/(2)`