Question

Geometry. Please help me. I need help ASAP .

Answer 1

a. (7, 5)

b. See answer below line

Explanation:

Focusing on A, we want to figure out how far away B is from P. To do this, let's divide the distance from A to P by 2 (since the ratio splits the segment so that AP = 2/5 of the entire segment). We'll then multiply that number by 3 (accounting for the other 3/5) and add the coordinate number from P to get the coordinate for B.

Let's first do this with the x-coordinates. P lies on x = 1 and A lies on x = -3. 1 and -3 are 4 units away from each other, so one half of 4 is 2. This means that B's x-coordinate is 3 * 2 units, or 6 units away from P horizontally. 1 + 6 = 7, so the x-coordinate is 7.

Let's do the same thing for the y-coordinates. P lies on y = 2 and A lies on y = 0. 0 and 2 are 2 units away from each other and 2/2 = 1, so B's y-coordinate is 3 * 1, or 3 units away from P vertically. 2 + 3 = 5, so the y-coordinate is 5. This means that B exists at (7, 5).

---------------------------------------------------

Now onto part B. I'll try to make this as short as possible. Let's find the slope of AP for starters:

`(2-0)/(1+3) = (2)/(4) = (1)/(2)`

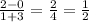
Next, let's make a slope-intercept form equation with point P:

`y=mx+b`

`2 = (1)/(2) (1) + b`

`2 = (1)/(2)  + b`

`2 - (1)/(2) = (1)/(2) - (1)/(2) + b`

`(3)/(2) = b`

`y=(1)/(2)x +  (3)/(2)`

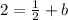
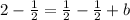
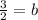
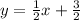
Finally, let's put the coordinates for B into our equation:

`5 = (1)/(2)(7) + (3)/(2)`

`5 = (7)/(2) + (3)/(2) = (10)/(2) = 5`

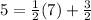
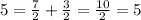
When the coordinates for B are placed into the expression, the expression is true. This means that the slope at the point B is the same slope as on the line AP. Part A also showed how we used AP to find the position of B, meaning that B is intersected by the line AP. Combined, these show that B lies on the line AP.