Question

QUESTION 1. Choose the point-slope form of the equation below that represents the line that passes through the points (−6, 4) and (2, 0). A) y − 4 = −one half(x + 6) B) y − 4 = 2(x + 6) C) y + 6 = −one half(x − 4) D) y + 6 = 2(x − 4) Question 2 (Multiple Choice Worth 2 points) Given the equation y − 3 = one half(x + 6) in point-slope form, identify the equation of the same line in standard form. A) x − 2y = −12 B) y = one halfx C) y = one halfx + 6 D) y = one halfx + 9

Answer 1

First question: C) y + 6 = -1/2 ( x + 6)

Second question A) x - 2y = -12

Explanation:

Question 1

First we calculate the slope:

m = (0-4)/(2+6) = (-4)/(8) = -1/2

Then we substitute in the formula

(y+6) = -1/2 (x+6)

Question 2

y - 3 = 1/2(x+6)

2(y-3) = x+6

2y -6 = x + 6

x - 2y = -12

Answer 2

1. The correct answer is A.

2. The correct answer is A.

Explanation:

1. The first step is to find the slope of the line. If we have the coordinates of two points that lie on the line we can use the formula

`m = (y_2-y_1)/(x_2-x_1)`,

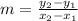where
`m` stands for the value of the slope, and the two points have coordinates
`(x_1,y_1)` and
`(x_2,y_2)`.

Then, substituting (−6, 4) and (2, 0) we have

`m = (0-4)/(2-(-6)) = (-4)/(8) = -(1)/(2).`

Recall that the point-slope equation of a line has the form

`y - y_1 = m(x-x_1)`

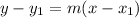
where
`m` stands for the slope and
`(x_1,y_1)` is any point of the line. Now, we found that
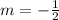`m = -(1)/(2)` and taking the point
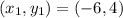`(x_1,y_1) = (-6,4)`, we substitute in the formula and obtain

`y-4 = -(1)/(2)(x+6)`.

Therefore, the point slope equation of the line is

`y-4 = -(1)/(2)(x+6).`

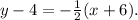
2. Recall that the standard equation of a line has the form
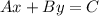`Ax+By =C`. Notice that only the equation in A. has this form. Anyway, let us check that, effectively, that A. is the correct answer.

The equation
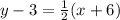`y-3 = (1)/(2)(x+6)` is equivalent to

`y-3 = (1)/(2)x+3`.

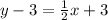This equality is equivalent to

`-6 = (1)/(2)x-y`.

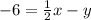Now, multiplying the whole equation by 2, we obtain

`-12 = x-2y`.

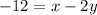The above identity is exactly the equation in A.