Answer:
The function
 is not a solution of the given differential equation.
is not a solution of the given differential equation.
Explanation:
Verify that a function f (x) is a solution to a differential equation, consists in finding the derivatives of the function and entering them into the equation. If the given function, indeed, is the solution, equality must be checked.
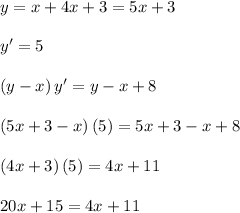
The function
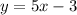 is not a solution of the given differential equation
is not a solution of the given differential equation