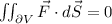Question

Use the Divergence Theorem to compute the surface integral Z Z T −→F · d −→S where T is the unit sphere x 2 + y 2 + z 2 = 1 and −→F (x, y, z) = hy, z, xi.

Answer 1

The answer is zero, because the divergence of the field is zero.

Explanation:

The vector field we have to integrate is:

`\vec F(x,y,z) = (hy,z,ix)`

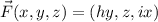
Where (I assume) h and i are just constants.

To use the divergence theorem, we first have to know what the divergence is.

The dvergence of a vector field is denoted:

`\\abla \cdot \vec F`

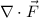
And it is equal to:

`\\abla \cdot \vec F = (\partial F_x)/(\partial x) + (\partial F_y)/(\partial y) + (\partial F_z)/(\partial z)`

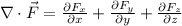
Where
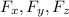`F_x , F_y , F_z` are the components of the vector field in the x, y and z direction respectively.

Now, what does the Divergence Theorem (or Gauss-Ostrogradsky Theorem) say?

It states that:

`\iint _(\partial V) \vec F \cdot d\vec S= \iiint_V \\abla \cdot \vec F \,  dV`

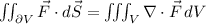
If F is a continiously differentiable vector field.

But, if we calculate the divergence of this vector field, we get zero! Let's check that.

`\\abla \cdot \vec F = (\partial (h \, y))/(\partial x) + (\partial z)/(\partial y) + (\partial (i\, x))/(\partial z) = 0+0+0=0`

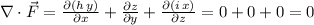
Now, if we insert this into the statement of the Divergence Theorem, we get that the surface integral is equal to the triple integral of zero over the interior of the surface. That integral is obviously zero, thus we have:

`\iint _(\partial V) \vec F \cdot d\vec S=0`