Answer:
y =
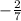 x + 4
x + 4

Explanation:
We are to find the equation of line 1 which passes through point (-4,6)
Line 1 is perpendicular to line 2.
The equation of line 2 is; y =
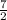 x + 5
x + 5
The slope of line 2 is
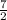
Because the product of two perpendicular line is -1;
The slope of line 1 is -1 ÷
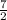 =
=
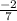
Taking another point (x,y) on line 1;
Slope = change in y ÷ change in x
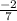 =
=
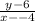
y - 6 =
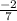 (x + 4)
(x + 4)
y - 6 =
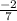 x -
x -

y =
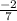 -
-
 + 6
+ 6
y =
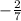 x + 4
x + 4
