Answer:
Ker(T) has basis
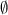
Range(T) has basis

Explanation:
If the matrix you wanted to represent is
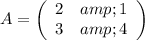 , then:
, then:
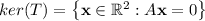 .
.
So, to find ker(T) you must solve the homogenous equation

Using Gauss elimination we obtain the simpler equivalent system
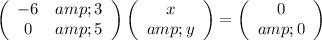
Then, we have that
 .
.
We have that
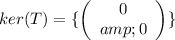 . On this case we say that the basis is the empty set
. On this case we say that the basis is the empty set
 .
.
The range of
 is the set of vectors of the form
is the set of vectors of the form
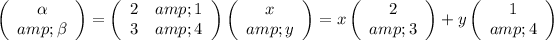
So,
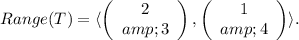 Where the angle brakets denotes the span.
Where the angle brakets denotes the span.