Answer: 0.0455
Explanation:
Given : Weekly demand at a grocery store for a breakfast cereal is normally distributed .
Population mean :
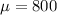
Standard deviation :
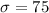
To find : Probability that the weekly demand is less than 650 boxes or greater than 950 boxes.
We first find z-score corresponds to 650 and 950.
Since

Then , for x= 650
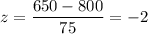
x=950
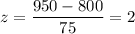
Then , the probability that the weekly demand is less than 650 boxes or greater than 950 boxes is given :-
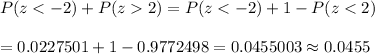
Hence, the probability that the weekly demand is less than 650 boxes or greater than 950 boxes = 0.0455