Question

Energy is generated uniformly in a 6 cm thick wall. The steady-state temperature distribution

T(z) = 145 + 3000z - 1500z^2

Where T is temperature measured in C, and z is the distance measured from one side of the walls in meters. Determine the rate of heat generation per unit volume if the thermal conductivity of the wall is 15 W/m.K.

Answer 1

Heat generation per unit volume is 45 KW.

Step-by-step explanation:

Given that

Thickness of wall = 6 cm

Temperature distribution

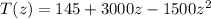`T(z)=145+3000z-1500z^2` -----1

K= 15 W/m.k

As we know that at steady state condition

`(d^2T)/(dz^2)+(q)/(K)=0` -----2

Where q is the heat generation per unit volume.

So from equation 1

`(dT)/(dz)=3000-3000z`

`(d^2T)/(dz^2)=-3000`

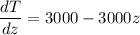
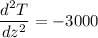
Now from equation 2

`(d^2T)/(dz^2)+(q)/(K)=0`

`-3000+(q)/(15)=0`

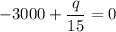
So q= 45 KW

So heat generation per unit volume is 45 KW.