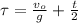Question

Ball A is thrown vertically upwards with a velocity of v0 . Ball B is thrown upwards from the same point with the same velocity t seconds later.

Part A

Determine the elapsed time t<2v0/g from the instant ball A is thrown to when the balls pass each other .

Express your answer in terms of some or all of the variables v0, t, and the acceleration due to gravity g .

Answer 1

The answer is
`\tau = (v_o)/(g) + (t)/(2)`

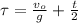
Step-by-step explanation:

If the ball is thrown vertically, the equation of its position is

`y(\tau) = y_0 + v_0\tau - (1)/(2)g\tau^2`

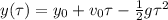
So setting our coordinate system in the position of throwing
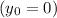`(y_0=0)`, the equation for A is

`y_A(\tau) = v_0\tau - (1)/(2)g\tau^2`

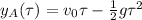
and for B

`y_B(\tau') = v_0\tau' - (1)/(2)g{\tau'}^2`

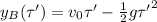
where

`\tau' = \tau - t`

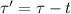
due to the delay of the throwing between A and B, "t"

`t = \tau - \tau'`.

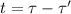Now, the balls passing each other means that

`y_B(\tau') = y_A(\tau)`

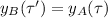
then

`v_0(\tau - t) - (1)/(2)g(\tau - t)^2 = v_0\tau - (1)/(2)g\tau^2`

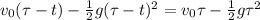
cancelling some terms...

`-v_0t + g\tau t - (1)/(2)gt^2 = 0`

so

`\tau = (v_o)/(g) + (t)/(2)`