Question

Stu Dent has 7 different math books, 5 different science books and 10 different engineering books. Find the number of ways to pick two books with different subjects.

Answer 1

155

Explanation:

Number of math books = 7

Number of science books = 5

Number of engineering books = 10

We need to find the number of ways to pick two books with different subjects.

Solution :

We will use combination here .

If we need to choose r objects from total n objects ,

`n_{C_(r)}=(n!)/(r!(n-r)!)`

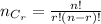
So, number of ways to pick two books of same subjects =
`7_{C_(2)}+5_{C_(2)}+10_{C_(2)}=(7!)/(2!5!)+(5!)/(2!3!)+(10!)/(2!8!)\\\\=(7* 6)/(2)+(5* 4)/(2)+(10* 9)/(2)\\\\=21+10+45=76`

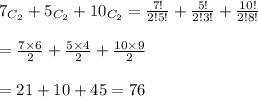
Also, number of ways to select any two books =
`22_{C_(2)}=(22!)/(2!20!)=(22* 21)/(2)=21* 11=231`

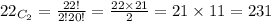
Therefore , number of ways to pick two books with different subjects =

number of ways to select any two books - number of ways to pick two books of same subjects = 231 - 76 = 155