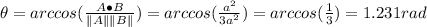Answer:
1.231 rad
Explanation:
Suppose that the vertex opposite the origin is (a, a, a), therefore, the geometric vector A = (a, a, a) is a diagonal of the cube. There are two opposite vertices (0, a, 0) and (a, 0, a), with which B = (a, 0, a) - (a, 0, a) = (a, -a, a) is the diagonal that intersects the first diagonal.
Now,