Question

❗❗❗❗HELP❗❗❗❗

Power usage is measured in kilowatt-hours, kWh. After 7 a.m., the power usage on a college campus increases at a rate of 21% per hour. Prior to 7 a.m., 15,040 kWh have been used. The university has a daily goal to keep their power usage less than or equal to 100,000 kWh.


Which of the following inequalities can be used to determine the number of hours, t, after 7 a.m. when the power usage on campus will be less than or equal to 100,000?


A: 15,040(1.021)t ≤ 100,000

B: 15,040(0.79)t ≤ 100,000

C: 15,040(1.21)t ≤ 100,000

D: 15,040(1.79)t ≤ 100,000

Answer 1

The correct option is C: 15,040(1.21)t ≤ 100,000

Explanation:

Consider the provided information.

It is given that after 7 a.m power usage on a college campus increases at a rate of 21% per hours.

Let t is the number of hours then the rate of increase will be:

`21\%t=(21)/(100)t=0.21t`

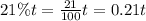
Prior to 7 a.m., 15,040 kWh have been used. Thus the increment of power use after t hours will be:

Increase=
`15,040(0.21)t`

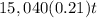
The total power consumption will be:

Previous power consumption + increase in power

`15,040+15,040(0.21)t\\=15,040(1+0.21)t\\=15,040(1.21)t`

The power usage on campus will be less than or equal to 100,000.

`15,040(1.21)t\leq 100,000`

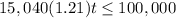
Hence, the required inequality is
`15,040(1.21)t\leq 100,000`.

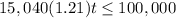Thus, the correct option is C: 15,040(1.21)t ≤ 100,000

Answer 2

The power increases by 21% per hour. 21% written as a decimal is 0.21.

Because it increases you would multiply the starting value by 1.21 times the number of hours (t).

That needs to be less than or equal to 100,00

The equation would be:

C: 15,040(1.21)t ≤ 100,000