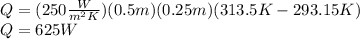Question

Air at 20oC flows over a flat plate of dimensions 50 cm x 25 cm. If the average heat transfer coefficient is 250 W/m2K, determine the steady rate of heat transfer from one side of the plate to air when the plate is maintained at 40oC.

Answer 1

Assumptions:

• Steady state.
• Heat transfer by convection.
• The temperature on the surface of the plate is constant and uniform.

Step-by-step explanation:

According to the attached image, the local heat flux over a flat plate can be expressed as follows,

`Q = (T_(s) - T_(\infty)) \ A_s \int\limit_{A_(s)} {h} \, dA_(s)`

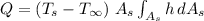
Where:

`Q : Local \ Heat \ Flux [W]\\T_(s) : Temperature \ on \ the \ surface \ of \ the \ plate \ [K]\\T_(\infty) : Temperature \ of \ the \ room \ [K]\\h : Convective coefficient [(W)/(m^2 K) ]\\A_(s) : Area \ of \ the \ plate [m^(2)]`

Consider an average convection coefficient,

`Q = \overline{h} \ A_(s) \ (T_s -T_(\infty))`

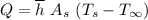
Answer:

Then, replacing all the values in the previous expression,

`Q = (250 (W)/(m^2 K) )(0.5m)(0.25m)(313.5K - 293.15K)\\Q= 625W`