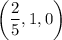Question

Find the point of intersection of the lines r(t) = (1, 0, 0) + t(−3, 5, 0) and s(t) = (0, 1, 1) + t(−2, 0, 5).

Answer 1

The point of intersection is:

`\displaystyle\left( (2)/(5), 1, 0\right)`

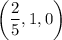
Step-by-step explanation:

Let us combine the vectors to get each equation in the format of a single vector, and we should use a different parameter for the second line, I will use k:

`\vec{r}(t)=\left< 1-3t, 5t, 0\right>, \vec{s}(k)=\left< -2k,1,1+5k\right>`

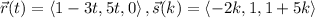
Then we set the x,y and z components of the equations, equal to each other:

`\begin{cases}1-3t=-2k\\5t=1\\0=1+5k\end{cases}`

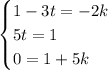
We have to solve that system of equations:

Solving the second and last for t and k we get:

`\begin{cases}1-3t=-2k\\t=\displaystyle(1)/(5)\\k=\displaystyle-(1)/(5)\end{cases}`

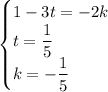
We plug them into the first equation and we get:

`\begin{cases}\displaystyle 1-3\cdot(1)/(5)=-2\cdot\left(-(1)/(5)\right)\\t=\displaystyle(1)/(5)\\k=\displaystyle-(1)/(5)\end{cases}`

Once we simplify:

`\begin{cases}\displaystyle (2)/(5)=(2)/(5)\\t=\displaystyle(1)/(5)\\k=\displaystyle-(1)/(5)\end{cases}`

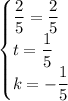
So, the system actually has those solutions we have found for t and k. We can now use any of the equations of the two lines. Plugging
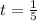`t=(1)/(5)` into the equation of the first line we get:

`\vec{r}(t)=\left< 1-3\left((1)/(5)\right), 5\left((1)/(5)\right), 0\right>=\left< (2)/(5), 1, 0\right>`

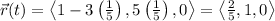
Therefore the point of intersection is:

`\displaystyle\left( (2)/(5), 1, 0\right)`