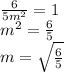Answer:
The answer is
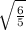
Explanation:
To calculate the volumen of the solid we solve the next double integral:
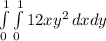
Solving:
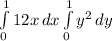
![[6x^(2) ]{{1} \atop {0}} \right. * [(y^(3))/(3)]{{1} \atop {0}} \right.](https://img.qammunity.org/2020/formulas/mathematics/college/t3f47582mz1z7n9lqjm0y7zymx0dqg89lf.png)
Replacing the limits:
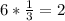
The plane y=mx divides this volume in two equal parts. So volume of one part is 1.
Since m > 1, hence mx ≤ y ≤ 1, 0 ≤ x ≤

Solving the double integral with these new limits we have:
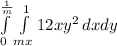
This part is a little bit tricky so let's solve the integral first for dy:
![\int\limits^(1)/(m)_0 [{12x (y^(3))/(3)}]{{1} \atop {mx}} \right.\, dx =\int\limits^(1)/(m)_0 [{4x y^(3 )]{{1} \atop {mx}} \right.\, dx](https://img.qammunity.org/2020/formulas/mathematics/college/qt87j7hor1xjsktrd3wv9yr5yg9ophgj60.png)
Replacing the limits:
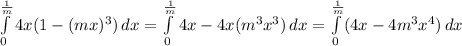
Solving now for dx:
![[{(4x^(2))/(2) -(4m^(3) x^(5))/(5) ]{{(1)/(m) } \atop {0}} \right. = [{2x^(2) -(4m^(3) x^(5))/(5) ]{{(1)/(m) } \atop {0}} \right.](https://img.qammunity.org/2020/formulas/mathematics/college/a3q4t2g0p3qjq0jjzkg2wmab7ayg1sdfzl.png)
Replacing the limits:
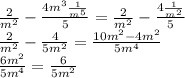
As I mentioned before, this volume is equal to 1, hence: