There are a few more than three, so they're really asking for the three they taught you already.
Usually we start with slope-intercept form, slope m, y intercept b
y = mx + b
The form in the question is called standard form or Cartesian form. Ironically, there are two different standard forms:
ax + by + c = 0
ax + by = c
They're more or less the same; pick the one your teacher likes. Next comes point-slope form. The line through point (a,b) with slope m is
y - b = m(x-a)
There's also point-point form. Given two points on the line (a,b) and (c,d) the line that joins them is
(c-a)(y-b)=(d-b)(x-a)
That's about it for the non-parametric forms. There are also parametric forms which generalize to higher dimensions.
The parametric point-point form says the line joining (a,b) and (c,d) is
(x,y)=(1-t)(a,b) + t(c,d)
t is a parameter which sweeps over the reals to generate the line. When the linear factors add up to one like that, it's called an affine combination.
Similarly, given a point (a,b) and a direction vector (m,n) we can write the line in point-direction vector form.
(x,y)=(a,b) + t(m,n)
I could probably come up with one or two more, but those are the main ones.
What's the slope of
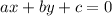
We solve for y:
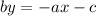
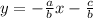
That line has slope -a/b. Of course if b is zero we say there's no slope.
Standard form handles the vertical line case here, so is often superior to the slope forms.