Answer:
-1/2
Explanation:
One way: Since both sides have absolute value, you could square both sides to get rid of the absolute value. This will result in a possible quadratic given the degrees inside the squares; I can already tell you know in this cases the variable squares will cancel since the coefficient of x on both sides inside the | | are the same.
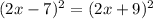
Expand both sides using:
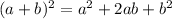 .
.
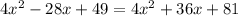
Subtract
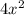 on both sides:
on both sides:
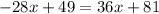
Add
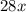 on both sides:
on both sides:
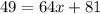
Subtract
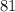 on both sides:
on both sides:
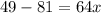
Simplify:
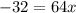
Divide both sides by 64:
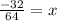
Reduce the fraction by dividing top and bottom by
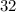 :
:
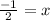
The solution is -1/2.
Let's check it.
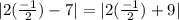
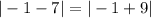
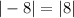
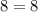
So x=-1/2 does check out.
Another way: This is for all the people who hate quadratics.
We could consider cases. These cases must be checked.
 is
is
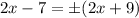
Let's solve all four of these and then check the solutions.
2x-7=2x+9
Subtract 2x on both sides:
-7=9 (not possible)
Moving on.
2x-7=-(2x+9)
Distribute:
2x-7=-2x-9
Add 2x on both sides:
4x-7=-9
Add 7 on both sides
4x=-2
Divide both sides by 4:
x=-2/4
Simplify:
x=-1/2
We already checked this from before.