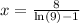Answer:
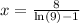
Explanation:
I will make an assumption.
We are trying to solve:
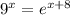
We first need to have the same base on both sides. So I'm going to write
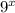 as
as
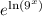 using that natural log (ln( )) and e^() are inverses.
using that natural log (ln( )) and e^() are inverses.
So we are going to rewrite the equation:
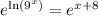
So now that the bases are the same we can set the exponents equal like so:
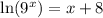
Using power rule we can bring down the x in front of ln( ):
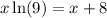
Now we need to get our terms with x on one side and terms without x on the opposite side. To do this, we just need to subtract x on both sides in this case:
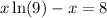
Factor the left hand side like:
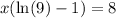
Now divide both sides by what x is being multiplied by: