Question

A salesperson's weekdy paycheck is 25% more than a second salesperson's paycheck. The two paychecks total $1425. Find the amount of each paycheck.

Answer 1

The paycheck of the first salesperson's is 791.67$ while the paycheck of the second salesperson's is 633.33$

Explanation:

Let:

x: First salesperson's weekday

y: Second salesperson's weekday

So, we know that a salesperson's weekday paycheck is 25% more than a second salesperson's paycheck, this can be written as:

`x=y+(25 \%)y \\ \\ x=y+0.25y \\ \\ x=1.25y`

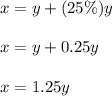
We also know that the two paychecks total $1425, so this can be written as:

`x+y=1425`

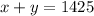
By using substitution method:

`(1) \ x=1.25y \\ \\ (2) \ x+y=1425 \\ \\ Substituting \ 1 \ into \ 2: \\ \\ 1.25y+y=1425 \\ \\ Combining \ like \ terms: \\ \\ 2.25y=1425 \\ \\ Isolating \ y: \\ \\ y=(1425)/(2.25)=633.33 \\ \\ Finding \ x, from \ 2: \\ \\ x=1425-633.33=791.67`

Finally:

The paycheck of the first salesperson's is 791.67$ while the paycheck of the second salesperson's is 633.33$