Question

HI(g) decomposes to molecular hydrogen and molecular iodine by a

second-order reaction. If the initial pressure of Hl is 0.691 atm and
the rate constant for the reaction is 0.100 atm-1.min-1, how much
time (min) will pass before the HI pressure drops to 0.187 atm?
Enter your answer to 1 decimal place.

Answer 1

• 39.0 min

Step-by-step explanation:

Second order decomposition (1 reactant) reaction means:

• rate = - d {HI] / dt = k [HI]² =

• Integrating:

`\int\limits^([HI_1])_([HI_0]) {\,(d[HI])/([HI]^2)=-\int\limits^t_0 {t} \, dt`

`(1)/([HI_t])-(1)/([HI_0])=kt`

When temperature and volume are kept constant concentration is proportional to pressure (P) and the rate may be expressed in terms of pressure as:

`(1)/(P_t)-(1)/(P_0)=kt`

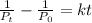
Here you have:

• t = ?

• P at t = 0 = 0.691 atm

• P at t = t = 0.187 atm

• K = 0.100 atm⁻¹ . min⁻¹

Therefore, substituting:

• 1 / 0.187atm - 1 / 0.691atm = 0.100 atm⁻¹ . min⁻¹ . t

• t = 3.900atm⁻¹ / 0.100 atm⁻¹ min⁻¹

• t = 39.0 min ← answer