Question

20. An electron with total energy 5 eV approaches a potential barrier of height 20 eV. If the probability that the electron tunnels across the barrier is 0.03, what is the width L of the barrier? a. 0.0116 nm b. 0.116 nm c. 1.16 nm d. 11.6 nm e. 116 nm Spring 2009 21. Define K UE

Answer 1

The width L of the barrier is b. 0.116nm

Step-by-step explanation:

This is a case of tunnel effect when the probability is less than one.

First of all you find all the information the problem gives you:

Electron's total energy E=5eV

Height of potential barrier U=20eV

Crossing Probability T=0.03

Width of the barrier L=unknown

Then you need to find the equations to use in cases in which the probability is less than 0, so you have:

`T=Ge^(-2kL)`

`G=16(E)/(U)(1-(E)/(U))`

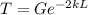
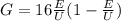
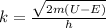`k=(√(2m(U-E)))/(h)` where m is the mass of the electron,
`m=9.11*10^(-31)Kg`, and h is the Planck constant,
`h=1.054*10^(-34)J.s`

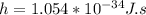
First we find G, we have:

`G=16((5.0eV)/(20eV))(1-(5.0eV)/(20eV))`

`G=4(1-0.25)=3`

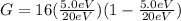
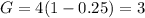
Now, to solving k, we need to find the difference (U-E) :

U - E = 20eV - 5eV = 15eV

`15eV*(1.60218*10^(-19)J)/(1eV) =2.403*10^(-18)J`

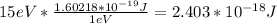
Then, we can find k:

`k=(√(2m(U-E)))/(h)`

`k=\frac{\sqrt{2(9.11*10^(31)kg)(2.403*10^(-18)J)}}{1.054*10^(-34)(J)/(s)}`

`k=1.98*10^(10)`

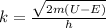
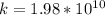
Finally, we solve for L the probability equation T:

`T=Ge^(-2kL)`

`(T)/(G)=e^(-2kL)`

`ln((T)/(G))=ln(e^(-2kL))`

`ln((T)/(G))=-2kL`

`L=(ln((T)/(G)))/(-2k)`

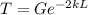
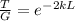
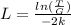
And replacing values for T, G and k, we can find the width of the barrier:

`L=(ln((0.03)/(3)))/(-2(1.98*10^(10)))m`

`L=1.16*10^(-10)m*(1*10^(9)nm)/(1m)`

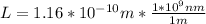
L=0.116nm