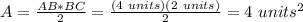Answer:
1) It is a right triangle.
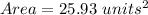
2) It is a right triangle.
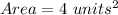
The points of each triangle are plotted in the images attached.
Explanation:
1) The points
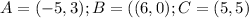 are plotted in the first image attached.
are plotted in the first image attached.
Knowing the points of the triangle, you can find the slope of
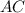 and
and
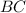 with this formula:
with this formula:

Then:


Since the slopes of the sides
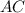 and
and
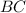 are negative reciprocals, they are perpendicular; therefore IT IS A RIGHT TRIANGLE.
are negative reciprocals, they are perpendicular; therefore IT IS A RIGHT TRIANGLE.
Find the length of
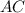 and
and
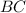 in order to calculate the area of the triangle:
in order to calculate the area of the triangle:
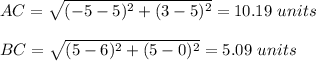
The area is:
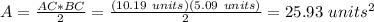
2) The points
 are plotted in the second image attached.
are plotted in the second image attached.
By definition horizontal and vertical lines are perpendicular, therefore IT IS A RIGHT TRIANGLE.
You can observe in the figure that the lenghts of the sides
 and
and
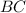 are:
are:
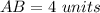
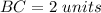
Therefore, the area is: