Question

At an accident scene on a level road, investigators measure a car’s skid mark to be 88 m long. The accident occurred on a rainy day, and the coefficient of kinetic friction was estimated to be 0.42. Use this data to determine the speed of the car when the driver slammed on (and locked) the brakes. Use the work-energy principle to solve this problem. (While you are doing the problem think about why the car’s mass does not matter.)

Answer 1

Answer:27 m/s

Step-by-step explanation:

Given

car's skid length is 88 m long

coefficient of kinetic friction is 0.42

let the mass of car be m and v be the velocity with which it was running initially.

Friction force
`=\mu mg=0.42* m* g`

work done by friction force =change in the kinetic energy of car

work done by Friction
`=\mu mg\cdot L=\mu mg * 88cos(180)`

Change in the Kinetic Energy
`=0-(1)/(2)mv^2`

`\mu mg * 88cos(180)=0-(1)/(2)mv^2`

`0.42* m* g=(1)/(2)m(v)^2`

`v=√(2* 0.42* 9.81* 88)=√(725.155)=26.92 \approx 27 m/s`

Mass of car does not matter because in the final expression m gets cancelled.

Answer 2

The the speed of the car is 26.91 m/s.

Step-by-step explanation:

Given that,

distance d = 88 m

Kinetic friction = 0.42

We need to calculate the the speed of the car

Using the work-energy principle

work done = change in kinetic energy

`W=\Delta K.E`

`\mu\ mg* d=(1)/(2)mv^2`

`v^2=2\mu g d`

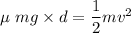
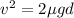
Put the value into the formula

`v=√(2*0.42*9.8*88)`

`v=26.91\ m/s`

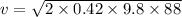
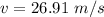
Hence, The the speed of the car is 26.91 m/s.