Question

the area of ABED is 49 square units. Given the AG=9. and AC=10 units whay fraction of the are ACIG is represented by the shaped region? ​

Answer 1

The fraction of the area of ACIG represented by the shaped region is 7/18

Explanation:

see the attached figure to better understand the problem

step 1

In the square ABED find the length side of the square

we know that

AB=BE=ED=AD

The area of s square is

`A=b^(2)`

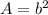
where b is the length side of the square

we have

`A=49\ units^2`

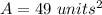
substitute

`49=b^(2)`

`b=7\ units`

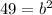
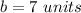
therefore

`AB=BE=ED=AD=7\ units`

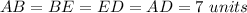
step 2

Find the area of ACIG

The area of rectangle ACIG is equal to

`A=(AC)(AG)`

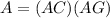
substitute the given values

`A=(9)(10)=90\ units^2`

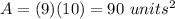
step 3

Find the area of shaded rectangle DEHG

The area of rectangle DEHG is equal to

`A=(DE)(DG)`

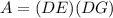
we have

`DE=7\ units`

`DG=AG-AD=9-7=2\ units`

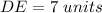
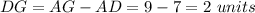
substitute

`A=(7)(2)=14\ units^2`

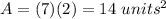
step 4

Find the area of shaded rectangle BCFE

The area of rectangle BCFE is equal to

`A=(EF)(CF)`

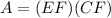
we have

`EF=AC-AB=10-7=3\ units`

`CF=BE=7\ units`

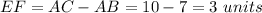
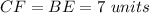
substitute

`A=(3)(7)=21\ units^2`

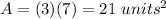
step 5

sum the shaded areas

`14+21=35\ units^2`

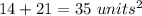
step 6

Divide the area of of the shaded region by the area of ACIG

`(35)/(90)`

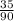
Simplify

Divide by 5 both numerator and denominator

`(7)/(18)`

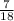
therefore

The fraction of the area of ACIG represented by the shaped region is 7/18