Question

Without using calculus or any other advanced math, the MS Solver plug-in can be used to find the input value for x that results in a maximum value for a function f(x). The price x is in the Solver "variable cell" and the function 1000x – 300x^2 is the Solver "objective." Question: What is the price x that maximizes weekly revenues?

Answer 1

The weekly revenue is maximum at x=1.67.

Step-by-step explanation:

The given function is

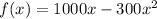`f(x)=1000x -300x^2` .... (1)

where, f(x) is the total revenue at price x.

We need to find the price x at which the weekly revenue is maximum.

The leading coefficient of the given function is -300, which is a negative number. So, it is a downward parabola and vertex of a downward parabola is the the point of maxima.

If a parabola is defined as

`g(x)=ax^2+bx+c` ... (2)

then the vertex of the function is

`(-(b)/(2a),g(-(b)/(2a)))`

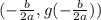
From (1) and (2) it is clear that

`a=-300,b=1000, c=0`

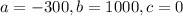
The given function is maximum at

`-(b)/(2a)=-(1000)/(2(-300))`

`-(b)/(2a)=(10)/(6)`

`-(b)/(2a)=1.66667`

`-(b)/(2a)\approx 1.67`

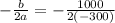
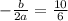
Therefore the weekly revenue is maximum at x=1.67.