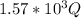Answer:
Step-by-step explanation:
The volume charge density is defined by ρ =
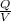 (Equation A), where Q is the charge and V, the volume.
(Equation A), where Q is the charge and V, the volume.
The units in the S.I. are
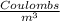 , so we have to express the radius in meters:
, so we have to express the radius in meters:
inner radius =
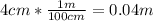
outer radius =
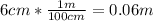
Now, we know that the volume of the sphere is calculated by the formula:
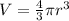 , and as we have an spherical shell, the volume is calculated by the difference between the outher and inner spheres:
, and as we have an spherical shell, the volume is calculated by the difference between the outher and inner spheres:
V =
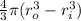 , where
, where
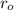 is the outer radius and
is the outer radius and
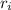 is the inner radius.
is the inner radius.
Replacing the volume formula in the Equation A:
ρ =
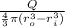
ρ =
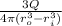
Replacing the values of the outer and inner radius whe have:
ρ =
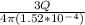
ρ =