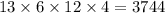Question

A poker hand consists of five cards selected from a 52 card deck. The order of the cards in a poker hand does not matter. A poker hand is called a full house if it has two cards of one rank and three cards of a second rank. For example, a hand consisting of two 7’s and three queens is a full house. How many different full house hands are there?

Answer 1

Answer: 3744

Explanation:

Given : Total card in a deck = 52

The total number of ranks in a deck = 13

Then, the number ways to select a rank = 13

One rank = 4 cards of same rank.

Now, first we need to select two cards of same rank then, the number of ways for this =
`^4C_2=(4!)/(2!(4-2)!)=6`

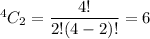
Now, the remaining ranks = 12

Again, The number ways to select a rank = 12

Next , we need to select 2 cards of same rank then, the number of ways for this =
`^4C_1=(4!)/(1!(4-1)!)=4`

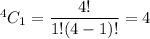
Now, the number of different full house hands are there :_

`13*6*12*4=3744`