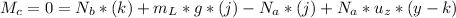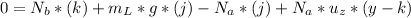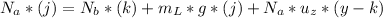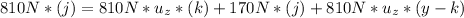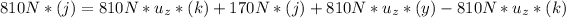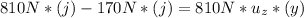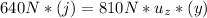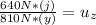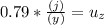Answer:
What is the magnitude of the force of the wall on ladder?
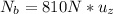
What is the magnitude of the normal force of the ground on ladder?

What is the minimum coefficient of friction so the ladder does not slip?
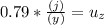
Step-by-step explanation:
Well, there are some variables that we are missing, but if you have them, just substitute them in the places of the equations, according to the drawing I attached.
We don't have the distance x or y, nor the angle o, this will be important later, so remember that the equations will need you to change the values to give you the answer.
The data we do have is:
Longitude of the ladder=5.9m
mass of the person:
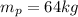
mass of the ladder:
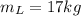
We are assuming that the person p is standing at a point that is horizontally from A, that we will call j, and vertical from B that we will call k.
Also the force of weight of the ladder is concentrated in A.
Some last things to consider, we are approximating g to 10
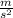 to simplify the calculations and since the wall if frictionless, then
to simplify the calculations and since the wall if frictionless, then
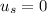
The last thing to do is to actually run the calculations:
What is the magnitude of the normal force of the ground on ladder?
For this we work with the sum of forces in the y-axis of the whole system:
∑
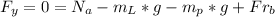
 but
but
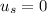
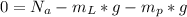
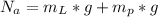
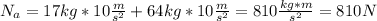

What is the magnitude of the force of the wall on ladder?
For this we work with the sum of forces in the x-axis of the whole system:
∑
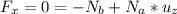
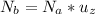
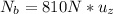
What is the minimum coefficient of friction so the ladder does not slip?
For this we work with the sum of momentum in the point where the person is standing:
∑