Question

Which will result in a difference of squares? (negative 7 x + 4)(negative 7 x + 4) (negative 7 x + 4)(4 minus 7 x) (negative 7 x + 4)(negative 7 x minus 4) (negative 7 x + 4)(7 x minus 4)

Answer 1

Option C

Explanation:

Answer 2

(negative 7 x + 4)(negative 7 x minus 4)

Explanation:

Consider two real numbers a and b. A difference of squares involving a and b is usually given as;

`a^(2)-b^(2)`

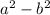
The difference of the two squares above can be factored to yield;

`(a-b)(a+b)`

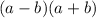
This implies that in order to have the difference of squares we must have a product involving the difference and the sum of the numbers.

The expression;

(negative 7 x + 4)(negative 7 x minus 4) can also be written as ( 4 - 7x) ( -4 - 7x)

( 4 - 7x) ( -4 - 7x) = ( 4 - 7x) (-1( 4 + 7x)) = -1 *( 4 - 7x) ( 4 + 7x)

Expanding the last expression yields;

-1 (16 + 28x -28x - 49x^2) = -1 (16 - 49x^2) = 49x^2 - 16 which is in deed a difference of squares