Question

Please provide the answer and an explanation.

Answer 1

A = 37.1 square cm

Explanation:

Composite Figures

The image shows a figure that can be seen as a composition of three regular shapes: two identical rectangles and a quarter of a circle.

The area of a rectangle of dimensions W and L is:

Ar = WL

And the area of a circle of radius r is:

`Ac =\pi r^2`

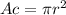
A quarter of a circle has an area of:

`\displaystyle A_q =(\pi r^2)/(4)`

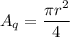
The rectangles have dimensions of 5 cm by 3 cm, thus the area is:

Ar = 5 cm * 3 cm = 15 square cm

The quarter of a circle has a radius of r=3 cm, its area is:

`\displaystyle A_q =(\pi 3^2)/(4)`

Calculating:

`\displaystyle A_q =7.07\text{ square cm}`

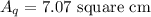
The total area is twice the area of each rectangle plus the area of the quarter of a circle:

A = 2*15 + 7.07

A = 37.07 square cm

To the nearest tenth:

A = 37.1 square cm