Question

The minimum distance between two fence posts is 4 feet. The maximum distance is 10 feet. A. Represent these two distances on a number line. B. Write an absolute value equation that represents the minimum and maximum distances

Answer 1

Part A) The number line in the attached figure

Part B) The absolute value equation is
`\left|x-7\right|=3`

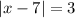
Step-by-step explanation:

Part A) Represent these two distances on a number line

we know that

The minimum distance between two fence posts is 4 feet, and the maximum distance is 10 feet

Let

x ----> the distance between the two fence post

so

`4\leq x \leq 10`

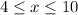
The interval is -------> [4,10]

using a graphing tool

see the attached figure

In a number line the solution is the shaded area at right of x=4 (close circle) and at the left of x=10 (close circle)

Part B) Write an absolute value equation that represents the minimum and maximum distances

Find the midpoint of the interval [4,10]

`M=((x1+x2)/(2))`

substitute the values

`M=((4+10)/(2))`

`M=(7)`

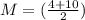
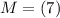
The distance from the midpoint to the endpoints of the interval is 3 feet

so

The absolute value equation is

`\left|x-7\right|=3`

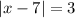
Verify

Solve the absolute value

case 1) positive value

`+(x-7)=3`

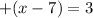
Solve for x

`x=7+3=10\ ft` ----> maximum distance

case 2) negative value

`-(x-7)=3`

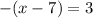
Solve for x

`-x+7=3`

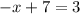
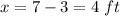`x=7-3=4\ ft` ----> minimum distance