Based on the given information on the cylinder, the change in entropy of the gas is approximately -6.48 J/K.
How to determine the change in entropy of the gas
To determine the change in entropy of the gas, use the first law of thermodynamics, which states that the change in internal energy (ΔU) of a system is equal to the heat (Q) added to the system minus the work (W) done by the system:
ΔU = Q - W
Since the gas temperature remains constant at 20 °C, we can assume that there is no heat transfer (Q = 0) and the change in internal energy is solely due to the work done on the gas:
ΔU = -W
Given that the work done on the gas by the compression is 1.9 ×
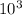 J, we have:
J, we have:
ΔU = -1.9 ×
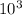 J
J
The change in entropy (ΔS) of the gas can be calculated using the equation:
ΔS = ΔU / T
where T is the temperature in Kelvin.
Since the gas and surroundings are both at 20 °C, convert it to Kelvin:
T = 20 + 273.15 = 293.15 K
Now calculate the change in entropy:
ΔS = (-1.9 ×
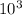 J) / 293.15 K
J) / 293.15 K
ΔS ≈ -6.48 J/K
The change in entropy of the gas is approximately -6.48 J/K.