Answer:
The standard deviation would stay the same
Step-by-step explanation:
Given:
Salaries as:
$3,500
$4,000
$4,500
and after $100 raise
$3,600
$4,100
$4,600
The average of the salaries before raise
= ( $3,500 + $4,000 + $4,500 ) / 3 = $4,000
The standard deviation =

and
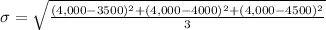
or
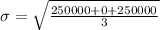
or
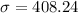
and, after the raise
the average = ( $3,600 + $4,100 + $4,600 ) / 3 = $4,100
now,
the standard deviation ,
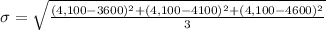
or
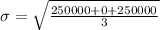
or
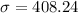
therefore, The standard deviation would stay the same