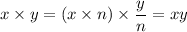Question

Harris said that 15 X 9 is equivalent to 45 X 3 because you can multiply one dimension by three and divide the other dimension by three. His partner said that only works when you double one number and halve the other. Who is right? Explain.

Answer 1

Harris is right.

Explanation:

`15* 9 = 45* 3 = 135`

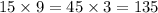
What actually happened was:

`15* 3 = (15* 3)* (9 / 3) = 135`

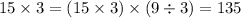
Another way to explain this is the associative property of multiplication:

`(a* b)* c = a* (b* c)`

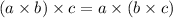
This is also possible when we multiply one dimension by 2 and divide the other by 2.

But, it is true for all numbers.

If we multiply one dimension by n and divide the other by n, the anser remain the same.

`x* y = (x* n)* \displaystyle(y)/(n) = xy`

Answer 2

Harris is right

Explanation:

The factors in a product can be grouped any way you like. That is the meaning of the associative property of multiplication.

15×9 = 15×(3×3) = (15×3)×3 = 45×3