Question

Sam owns a corn dog stand. He has found that his daily profit is represented by the equation P(x) = - x² + 12x + 43 with P being profits and x being the number of corn dogs sold. What is the most he can earn in a day?

Answer 1

He can earn $79

Explanation:

The maximun benefic that he can earn is represented by the tangent of the function when his value is zero.

Writing the function: P(x)= -
`x^(2)`+12x+43, now we have to derivate

P´(x)= -2x + 12.

To have the maximun profit we do P´(x)=0

0=-2x+12⇒ 2x=12 ⇒ x=12/2 ⇒ x=6

The next step is replace this value on the P(x)

P(6)= -
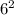`6^(2)`+12*6+43

P(6)= $79