Question

Which two functions are inverses of each other?

Of(x) = x, g(x) = -x
of(x) = 2x, g(x) = -X
f(x) = 4x, 8(x) = x
O Mx) = -8x, 8(x) = 8x

Answer 1

Inverse is the opposite.

A negative value is an inverse of the same positive value and a positive value is an inverse of the same negative value.

Examples:

-2 is the inverse of 2

5 is the inverse of -5

The answer is:

f(x) = x, g(x) = -x

f(x) = -8x, g(x) = 8x

Answer 2

Option 3

Explanation:

We have to find, which two functions are inverses of each other?

Solution :

Two functions are inverse when the condition is fulfilled,

f(g(x))=x=g(f(x))

Applying in all options,

1) f(x)= x, g(x) = -x

`f(g(x))=f(-x)=-x\\eq x`

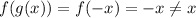
Not true.

2) f(x)= 2x, g(x) = -\frac{1}{2}x

`f(g(x))=f(-(1)/(2)x)=2*(-(1)/(2)x)=-x\\eq x`

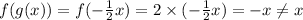
Not true.

3) f(x)= 4x,
`g(x) = (1)/(4)x`

`f(g(x))=f((1)/(4)x)=4*((1)/(4)x)=x`

`g(f(x))=f(4x)=(1)/(4)* 4x=x`

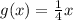
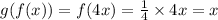
i.e. f(g(x))=x=g(f(x)) is true.

So, These two functions are inverse of each other.

4) f(x)= -8x, g(x) =8x

`f(g(x))=f(8x)=8*(-8x)=-64x\\eq x`

Not true.

Therefore, Option 3 is correct.