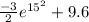Question

It is estimated that t-weeks into a semester, the average amount of sleep a college math student gets per day S(t) decreases at a rate of −3tet2 hours per day. When the semester begins, math students sleep an average of 8.1 hours per day. What is S(t), 15 week(s) into the semester?

Answer 1

To find the average amount of sleep a college math student gets per day, we need to integrate the given rate of change function. Given that the semester begins with math students sleeping an average of 8.1 hours per day, we can plug this value into the integral and evaluate it at t = 15 weeks.

Step-by-step explanation:

To find the average amount of sleep a college math student gets per day using the given information, we need to integrate the given rate of change function.

The rate of change function, −3tet^2, represents the rate at which the average amount of sleep decreases. To find the average amount of sleep at any given time 't', we need to integrate this function from the beginning of the semester to 't'.

Given that the semester begins with math students sleeping an average of 8.1 hours per day, we can plug this value into the integral and evaluate it at t = 15 weeks:

S(t) = ∫[0 to t] (-3te*t^2) dt + 8.1

S(15) = ∫[0 to 15] (-3te*t^2) dt + 8.1

Answer 2

s(15)=
`(-3)/(2) e^{15^(2) } +9.6`

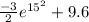
Step-by-step explanation:

Before to getting started ,we have to consider the function which represents sleep decline rate S'(t) =
`-3te^{t^(2) } \\`

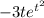
Since this function is interpreted in this case as a rate of change, we can deduce this funcion is the first derivative of the function of average amount of sleep (S(t)).

In order to find S(t), we will integrate S'(t)

`\int\limits^ {} -3t3e^{t^(2) } \, dx \\`

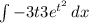
This case corresponds to intergration by substitution

Substituting u=
`x^(2) \\`

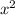
Computting the differential of u

`(du)/(dt) =2tdt\\`

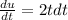
Now, let's go back to our integral and write it in terms of u, using both definition of u and its defferential.

`\int\limits^{}-3te^(u)  \, (1)/(2t)du  \\\\\int\limits^{}(-3)/(2) e^(u)du\\`

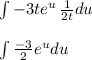
The integral of a exponential function is itself. So the result is:

`(-3)/(2) e^(u) +c`

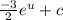
Now substitute u back in:

`(-3)/(2) e^{t^(2) } +c`

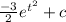
This answer correspond to function of average amount of sleep.

We know that when the semester begins (t=0) , math students sleep an average of 8.1 hours per day so we will use this info in order to find the value of c.

`s(0)=(-3)/(2) e^{0^(2) } +c=8.1\\\\(-3)/(2) +c=8.1`

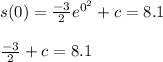
Solve this equation

c=8.1+
`(3)/(2)`

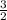
c=9.6

Replacing the value of c on S(t)

S(t)=
`(-3)/(2) e^{t^(2) } +9.6`

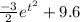
Now, let's to find the average of amount of sleep when 15 weeks has elapsed since the start date of the semester.

s(15)=
`(-3)/(2) e^{15^(2) } +9.6`