Question

Solve & Discuss It! Courtney and Malik are buying a rug to fit in a 50-square-foot space. Which rug should they purchase? Explain. $99 Rug Sale! T 7 ft x 7 ft 8 ft diameter 6 ft x 8 1/2 ft Rug Emporium has your floors covered.

Help me please

​

Answer 1

The first rug (7 ft x 7 ft) would be the most appropiate one since it fits in the room, only leaving a total uncovered area of 1 square foot to the sides.

Explanation:

1. Calculate the total area that the different rugs can cover.

a. 7 ft x 7 ft (square):
`Area=s^(2) =(7ft)^(2) =49ft^(2)`.

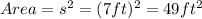b. 8 ft diameter (circle):
`Area=\pi r^(2) =\pi ((8ft)/(2) )^(2)=50.27ft^(2)`.

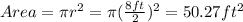Note. We substituted the radius (r) by the length of the diamateter divided by 2 because the radius is just half of the diamaterer in a circle.

c. 6 ft x 8 1/2 ft (square):
`Area=w*l=(6ft)(8.5ft) =51ft^(2)`.

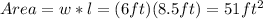2. Compare the total area that the different rugs can cover.

Taking into account that the room has an area of 50-square-foot, the 6 ft x 8 1/2 ft is not an option, since the rug is larger than the room. Also, the 8 ft diameter is barely larger than the room, so it isn't an option either. Therefore, the first rug, 7 ft x 7 ft, would be the most appropiate one since it fits in the room, only leaving a total uncovered area of 1 square foot to the sides.

-------------------------------------------------------------------------------------------------------

¿How much space is left uncovered?

If the room has a measure of 50 square-foot, the length of one side is
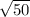`√(50)` . Now, the difference between the height of this room and the rug is, approximately,
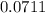`0.0711`. If the rug is placed in the center of the room, there will be a space of
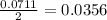`(0.0711)/(2)= 0.0356` feet between the walls and the rug for each side.